|
That Christ may dwell in your hearts by faith; that ye, being
rooted and grounded in love, May be able to comprehend with all saints what is
the breadth, and length, and depth, and height;
And to know the love of Christ,
which passeth knowledge, that ye might be filled with all the fulness of God.
Ephesians 3
Geometric points exist in spaces of different dimensionality, depending on how many numbers
are required to specify them.

A point in one dimension.
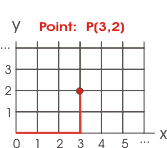
A point in two dimensions.
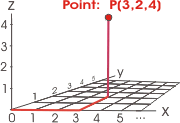
A point in three dimensions.
For example, to locate a point on a one-dimensional line, the x-axis, you
need only one number, the length x, to specify the exact position
of a point.
To locate a point on a two dimensional surface, the x-y plane, you need two numbers,
the length x and and breadth y.
Finally, to specify a point in three dimensional space,
you need three numbers, length x, breadth y, and height z.
The three points presented in the diagrams on the right are all related through a geometric
process called orthogonal projection. Consider the 3-dimensional point
represented by P(3, 2, 4). If we imagine shining light straight down the z-axis, the
shadow would fall on P(3, 2, 0) which corresponds to the Point P(3, 2) in the x-y
plane.
Likewise, if we were to shine light straight down the y-axis, the shadow of the
Point P(3, 2) would fall on P(3, 0), which corresponds to the one-dimensional Point
P(3), shown in the top diagram.
This is the mathematical formulation of how an object relates to its shadow
when the shadow is cast orthogonally, that is, at a right angle to the "sub-space"
of projection. Almost all projections we will be discussing are orthogonal, though there are some
interesting insights to be found by examining non-orthogonal projections.
When the dimensionality of the sub-space is one less than the original, the projection will be
called a "first-order projection." Thus, the projections
P(3, 2, 4) ==> P(3, 2)
P(3, 2) ==> P(3)
are both "first order" projections.
Definition: Second Order Projection:
When the dimensionality of the sub-space is two less than the orginal space, the projection will
be called a "second-order" projection. Thus, the projection
P(3, 2, 4) ==> P(3)
is a second order projection. It can be viewed as the result of two first-order projections:
P(3, 2, 4) ==> P(3, 2) ==> P(3)
These elementary ideas are important to this study of the geometry of Scripture because
highly significant
correlations emerge when the the Bible is viewed as a three-dimensional object.
To recognize the Bible as a 3D object, we simply note that each verse may
be located by specifying three numbers which indicate the Book, the Chapter, and the Verse.
This means that each verse corresponds to a unique point in
the three dimensional Euclidean space which mathematicians denote as R3.
Likewise, we can view the chapter structure of the Bible as forming a 2D space since each
chapter can be specified by two numbers, Book, and Chapter, and finally, we can
view the Canon of 66 Books as a one dimensional object.
To make this geometric view clear, I introduce a geometric notation as follows:
| Standard Notation |
Geometric Notation |
Dimensions |
|---|
| Genesis 1.1 |
PBible(1, 1, 1) |
3D |
| Isaiah 45 (entire chapter) |
PBible(23, 45) |
2D |
| Revelation (entire book) |
PBible(66) |
1D |
The symbol PBible(1,1,1) is read as Bible Point One, One, One.
The reason for writing
the word "Bible" as a subscript is so we can use the same notation to denote Points within
books, such as Isaiah.
For example, we have a two ways to refer to Isaiah 40.3:
PIsaiah(40, 3) = PBible(23, 40, 3)
Although both of these expressions refer to exactly the same verse, they represent the verse
in spaces of different dimensionality. PIsaiah(40, 3) represents the verse as a
Point in the two dimensional "plane" of Isaiah, whereas PBible(23, 40, 3)
represents the verse in the three dimensional "Bible Space."
There is nothing profound here at all ... yet. All we have done is present some definitions.
But if we actually read Isaiah 40.3, we will find something quite
astounding:
The voice of him that crieth in the wilderness, Prepare ye the way of the
LORD, make straight in the desert a highway for our God.
The first record of the fulfillment of this prophecy is found in Matthew 3.3, where we read:
For this is he that was spoken of by the prophet Esaias [Isaiah], saying,
The voice of one crying in the wilderness, Prepare ye the way of the Lord, make his
paths straight.
This verse located at PBible(40, 3, 3) projects onto
PBible(40, 3), and this coincides exactly with PIsaiah(40, 3)!
Consider what this means! The prophecy given in Isaiah 40.3 and its fulfillment in Matthew 3.3
are geometrically linked as a shadow to the object that casts it!
Identifying the common theme with the mnemonic phrase "The Voice Crying", we can display
this first-order projective link by writing:
| Link: The Voice Crying | PIsaiah( 40, 3 ) 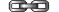 PBible( 40, 3 ) PBible( 40, 3 ) |
This link is not a KeyLink because other books also record the same event.
A graphic representation of this link is given in the article outlining the correlation
between Isaiah 40 and Matthew.
Not all projective links are first order. Second order links are the most common. They
display the simple geometric integration of the chapter sequence of some book of the Bible
with the order of the Canon. And although Isaiah presents the most complete
image of the Canon within the Canon, other books also echo the canonical structure.
For example, consider the verse that opens Matthew 22:
And Jesus answered and spake unto them again by parables,
and said, The kingdom of heaven is like unto a certain king, which made a
marriage for his son,
This corresponds to the theme of the 22nd book, the
Song of Songs. We have, therefore
a second order projective link between the chapter structure of Matthew and the
order of the Canon:
| Link: The Son's Marriage | PMatthew( 22 ) 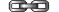 PBible( 22 ) PBible( 22 ) |
An outline of many of the projectve links between Matthew and the Canon are listed in
Correlations in Matthew.
Some projective links are made from phrases that occur exactly twice in
all of Scripture. These projective links are unique and act rather like the teeth in
a key or the tumbler of a combination lock. They provide incredible insight into the
supernatural structure of the Bible which now opens with a mere touch. These links are
called Keylinks.
One of my favorite examples of a first order projective Keylink is found by
searching the entire KJV for all occurences of the phrase "that ye may know and believe."
There are precisely two verses that contain this phrase. The first is found
in Isaiah 43.10:
Ye are my witnesses, saith the LORD, and my servant whom I have
chosen: that ye may know and believe me, and understand that I am he: before
me there was no God formed, neither shall there be after me.
The second in found in John 10.38 (vs. 37 is included for context):
If I do not the works of my Father, believe me not.
But if I do, though ye believe not me, believe the works: that ye may know,
and believe, that the Father is in me, and I in him.
Using geometric notation, John's verse is denoted as PBible(43, 10, 38).
This projects onto PBible(43, 10), and we have therefore
a first order projective Keylink uniting the two dimensional plane
of Isaiah to the shadow of the three dimensional Bible!
 | KeyLink: That Ye May Know and Believe | PIsaiah( 43, 10 )  PBible( 43, 10 ) PBible( 43, 10 ) |
An image of this KeyLink, and a discussion of its significance may be found in the
article entitled The Eternal I AM.
| 
