Statistical Probability of the Canon Wheel

One thing have I desired of the LORD, that will I seek after; that I may dwell in the house of the LORD all the days of my life, to behold the beauty of the LORD, and to enquire in his temple.

Psalm 27:4

The Canon Wheel

One would think it impossible miss the beauty and significance of the sevenfold symmetric perfection of the Canon Wheel. What could be simpler than a perfect Circle? What worthier design for God's Work than this universal symbol of Eternity, symmetrically divided in accordance with the fundamental numerical signature of Scripture - the Number Seven - embedded as a watermark throughout the text on all levels from Genesis to Revelation? And as if this weren't enough, the entire structure is supernaturally integrated with the 22 letters of the divine Hebrew alphabet - the original vector of revelation! Oh! Human language is utterly insufficient to communicate the perfection of the Holy Bible - words, sentences, paragraphs, indeed whole books - must needs overlap in the mind of the reader to see but a glimpse of God's infinite Wisdom and Knowledge radiating from Scripture. Of course, this is exactly what He has provided in the structure of His Word which is nothing less than infinity designed to be held in the palm of your hand, its fearful symmetry burning bright before your very eyes!

Yet not all have the gift of this vision. I therefore have answered the questions in the side box to reveal the absolute mathematical impossibility that this structure could have occurred by chance or even deliberate human effort. Of course, there is a certain futility and absurdity in presenting these arguments. It would be much simpler if the skeptic would merely ask God to open his eyes - like the blind men enlightened by Christ two thousand years ago. This has nothing to do with blind faith - on the contrary, it is the unbeliever who suffers blindness! The evidence is shining like the noontime sun in a cloudless sky! An analogy may help make this clear. It is rather like meeting a man who denies that Chinese is a language, and refuses to learn anything about it until it has been mathematically proven that the marks in the Chinese book are interrelated in the same way as other languages, and that they certainly were not randomly scratched out. The joke is that even if the proof is understood and accepted (a very unlikely outcome, considering the effect of wilful ignorance), the unbeliever has not come one step closer to knowing - let alone receiving - the message contained in the book! If, on the other hand, the unbeliever were willing to learn to read Chinese, the proof that it is indeed a language would simply fall out as an inevitable side effect. This analogy corresponds exactly with the Wheel. Its primary purpose is not mere proof that the Bible is the Word of God - what good would that do? It would be just like abstractly proving that Chinese really is a language to someone who refuses to learn. The person who chooses to learn, on the other hand, will gain all the benefit of the knowledge in the book while simultaneously receiving - as an inevitable side effect - absolute, irrefutable proof of the intelligent, purposeful design of the book.

How Many Possible Sevenfold Canons?

The Bible is divided into seven canonical divisions, starting with the 5 books of the Torah, 12 books of the Old Testament History, and so forth. This structure can be described by saying there is a canonical division D1 between books 5 and 6, another division D2 between books 17 and 18, and so forth. Six dividers are needed to describe seven divisions. The question of "How many possible sevenfold canons are there?" is therefore equivalent to asking "How many ways are there to put six dividers between 66 objects?"

This means that each possible sevenfold canonical division of the Bible can be represented as a line of 66 objects with six dividers dropped between them as follows:

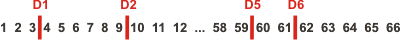
The number of sevenfold canonical divisions is therefore determined by the number of distinct ways there is to drop the six dividers between the 66 objects. This number is very easy to calculate - its a problem of Combinatorics . There are 65 places to drop the first division D1, 64 places to then drop the next division D2, 63 for the next, and so forth, so the total is ...

65 x 64 x 63 x 62 x 61 x 60 = 59,471,193,600 possible divisions.

Now rearrangement of the dividers amongst themselves - e.g. interchanging D1 with D2 - results in the same canonical division, so we need to divide by the total number of ways to arrange six objects which is simply 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720. The result is:

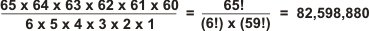
Numbers of this form are called Binomial Coefficients . They are also known as Choice numbers because they give the number of ways to select an unordered subset of k objects from a set of n objects. In the case above, it is called "65 choose 6" which tells us the number of ways to select an unordered subset of 6 dividers from the set of 65 dividers standing between each pair of books. This is simply an alternate description of our initial question. Note that similiar calculations are used to analyze the probability of the symmetric structure of the Old Testament canon alone [see Probabilities of the OT Symmetry].

Thus there are about 82 million possible sevenfold canonical structures of the Bible. Our task now is to determine how many of these exhibit both bilateral and radial symmetry.

How Many Symmetric Sevenfold Canons?

This answer to this question is essentially as simple as the one above, except that it involves a few "special cases."

1) Bilateral Symmetry demands that there be divisions between books 22 and 23 and 44 and 45. Otherwise a canonical division would cross from one Cycle to the next, which is not symmetric. For example, supposed that books 43 through 46 form a canonical division. These books are highlighted red in the image. They lack bilateral symmetry. Thus we must have two dividers as shown in the second image.

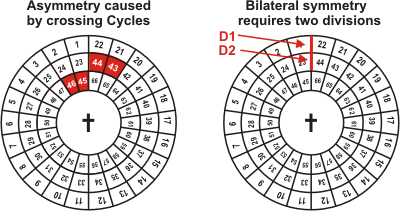
2) There now remains four dividers to place symmetrically on the Wheel. There are two possibilities we must consider.

• a) Suppose we drop D3 anywhere except on the line of bilateral symmetry, that is, between Spokes 11 and 12. Bilateral symmetry then demands that we place a corresponding divider in the mirror position. Radial symmetry demands that we place the remaining pair of dividers on the radii corresponding to the two just set or symmetrically in the same Cycle as the first two. Here are examples of each of these possibilities:

  

  
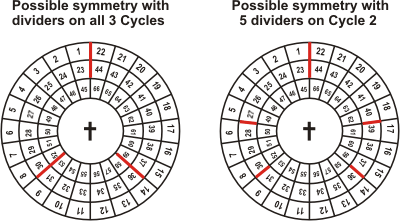
  We have 10 choices for where to drop D3 and its mirror D4. For each of these ten choices, we have these possibilities for D5 and D6:
  • i) Radial symmetry gives us only one choice if we drop D5 and D6 on a different Cycle.
  • ii) We have 9 choices if we drop D5 and D6 on the same Cycle as D3 and D4 since there are 18 open slots there.
  
  Total: 10 x 1 + 10 x 9 = 100.
   
  
• b) Now suppose we chose to place D3 on the line of bilateral symmetry. This leaves three dividers, so we need to place D4 in line with D3 since bilateral symmetry demands that all dividers not on the line of symmetry be paired - i.e. it must be an even number. D4 can be placed on either Cycle not holding D3, and for each of these choices, there remains two dividers that can be placed as a symmetric pair on any of the remaining 20 slots, giving 10 possibilities since interchanging D5 and D6 yields the same canonical division.
   
  Total: 2 x 10 = 20

Grand Total: 120 possible symmetric sevenfold canons. We can now use this number to determine the probability of "finding" a symmetric sevenfold canon.

Probability of a Symmetric Sevenfold Canon?

This probability is calculated by taking the ratio of the number of symmetric sevenfold canons (120) to the total number of possible sevenfold canons (82,598,880). The answer is one chance in 688,324.

When considering this number, it is extremely important to recall that the sevenfold structure designed by God can be derived from first principles using nothing but the Bible Wheel, two initial conditions, and symmetry constraints. This is exactly the same pattern that led to many of the most significant discoveries in 20th century Physics (cf. Fearful Symmetry).

How Many Canonical Orders?

This is another problem from the field of Combinatorics . The total number of ways to arrange n things is called n factorial, denoted by n!. It is calculated by forming the product of all numbers less than or equal to n:

n! = n x (n-1) x (n-2) x ... x 3 x 2 x 1

For example, the total number of ways to arrange the letters ABC is 3! = 3 x 2 x 1 = 6. This is easy to check by simply listing them:

ABC, ACB, BAC, BCA, CAB, CBA

The logic that gives rise to this formula is elementary. One simply notes that there are three choices for the first position, after which there remains two choices for the second position, and finally one for the last. Multiplying the number of choices yields the total number of ways one could arrange the three letters.

The answer to "How many ways are there to arrange the sixty-six books of the Bible?" is therefore:

66! = 66 x 65 x 64 x 63 x ... x 4 x 3 x 2 x 1 = 5.44 x 10⁹².

Written is standard decimal notation (to three significant digits), this number appears as:

544,000,000,000,000,000,000,000,000,000,000,000,000,000,000,
000,000,000,000,000,000,000,000,000,000,000,000,000,000,000.

This number is so far beyond all human experience that I hardly know how to describe it. It is 5.44 times 1 followed by 92 zeros! The implications of this are discussed in the next section.

Questions? Comments? Join the discussion on the Bible Wheel Forum!