Mathematical Derivation of the Canon Wheel
from First Principles

From whom the whole body fitly joined together and compacted by that which every joint supplieth, according to the effectual working in the measure of every part, maketh increase of the body unto the edifying of itself in love.

Ephesians 4:15f

One way to look at the Bible Wheel is as a scientific model of the structure of Scripture. Just as physical phenomena have been studied with various models such as Ptolemaic vs. Copernican Astronomy, Classical vs. Quantum Physics, and Newtonian vs. Relativistic Mechanics, so the Bible Wheel can be seen as a way to model the sixty-six books, the "data" of the Bible. What follows is a derivation of the sevenfold structure of the Christian Canon from first principles, using nothing but:

1. A Model
2. Two Initial Conditions
3. Two Symmetry Constraints

This follows precisely the same pattern as many of the greatest scientific discoveries of the last century, as discussed in my review of A. Zee's Fearful Symmetry. Let us begin:

Object to Model:

The traditional Protestant canon of 66 Books (the proto-canon of the Catholics).

Model:

Construct a circular grid of 66 Cells with 22 Spokes and three concentric circles called Cycles. Place the 66 books sequentially on the Wheel, so that Cycle 1 consists of Books 1 to 22, Cycle 2 consists of Books 23 to 44, and Cycle 3 consists of Books 45 to 66.

Method:

To derive the sevenfold structure of the Canon Wheel, impose two initial conditions and construct the Canon with the minimal number of divisions required to satisfy maximal symmetry constraints as explained below.

Definition:

A "canonical division" CD(m,c) is defined as a radial line between Spoke m and m+1 (modulo 22) on Cycle c (see the image below).

Definition:

The set of books contained between two canonical divisions CD(m,c) and CD(n,c) is defined as Block(m,n,c), where m denotes the starting division and n the ending division. For example, the Torah is Block(22,5,1) (see image below).

Initial Conditions:

History has given us two incontrovertible constraints on any possible canonical structure:

1. There must exist a canonical division between the first five books (The Torah) and the rest of Scripture.
2. There must exist a canonical division between the Old Testament and the New Testament.

Maximal Symmetry Constraints:

1. Bilateral Symmetry: The Wheel must look the same when reflected in mirror. This constraint demands that for each CD(m,c) there must exist a CD(n,c) such that m + n = 22.
2. Radial Symmetry: There must be no conflicting canonical divisions. Any two Cycles that contain canonical divisions must have the same number of divisions and all the divisions must lie on a common set of radii.

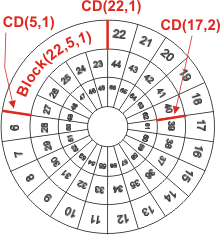
Construction:

Now construct the minimal Canon structure that satisfies the symmetry constraints:

1) The initial conditions demand that there are three canonical divisions.

There must be a CD(22,1) and a CD(5,1) to form Block(22,5,1) corresponding to the Torah.

There must be a CD(17,2) between the Old and the New Testaments.

2) Bilateral symmetry demands that there are two more canonical divisions to match the initial conditions:

There must be a CD(17,1) to match CD(5,1)

There must be a CD(5,2) to match CD(17,2)

3) Radial symmetry demands that there is one additional canonical division:

There must be a CD(22,2) to match CD(22,1).

The initial conditions and symmetry constraints are now satisfied. This is the minimal solution. Mapping these divisions on the Wheel results in the traditional Seven Canonical Divisions of the Christian Canon:

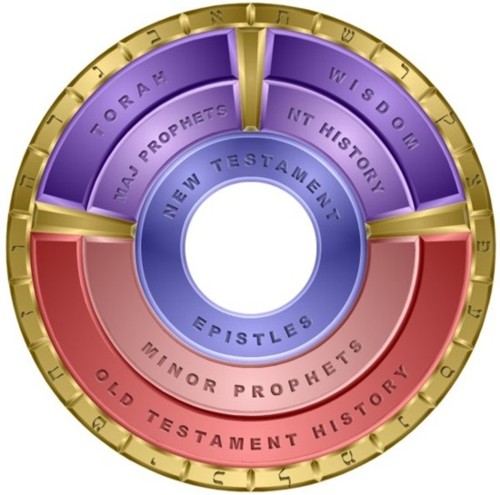
Questions? Comments? Join the discussion on the Bible Wheel Forum!